Different kinds of problems require different strategies to solve them. An approach that works great for one kind of problem fails miserably when applied to another kind of problem.
We know this intuitively. The saying, “If all you have is a hammer, every problem looks like a nail,” highlights our tendency to apply our favorite strategy, whether the problem fits or not (with the implied punch line that most problems aren’t nails, of course).
Wouldn’t it be nice if we could reliably determine in advance what kind of problem we’re facing and, therefore, what strategy is appropriate to solve the problem? 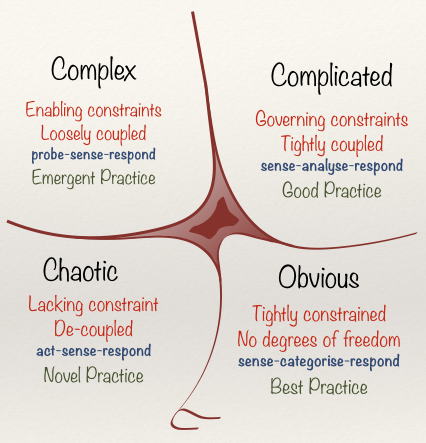 Enter Cynefin, complexity scientist Dave Snowden’s framework for making sense of problems and choosing the appropriate response. Cynefin makes some helpful distinctions about the complexity of different problems and has become one of our favorite tools for Agile leaders and teams.
Enter Cynefin, complexity scientist Dave Snowden’s framework for making sense of problems and choosing the appropriate response. Cynefin makes some helpful distinctions about the complexity of different problems and has become one of our favorite tools for Agile leaders and teams.
Cynefin divides the world of problems into four types (with a special space in the middle). Now, this isn’t a typical quadrant model, with two intersecting variables and a “good” quadrant you want to be in. It’s a sense making model, with fuzzy, context-specific boundaries and no one kind of problem better than the others—what matters is knowing where you are now so you can respond appropriately.
On the right side of the model are two kinds of problems we can call ordered. Ordered problems are ones where you can predict cause and effect in advance. You can make plans for ordered problems and, critically, have your plans actually work the way you expect.
On the left side of the model are two kinds of unordered problems. Unordered problems lack this predictability. They show emergence or randomness. The problem changes as you try to solve it.
Beginning in the bottom right, we have what Cynefin calls obvious problems. Obvious problems are ones you’ve seen and solved before, perhaps many times before. They have well known solutions (often what we’d call “best practices” or recipes). The relationship between cause and effect is known and predictable. Many operational or manufacturing problems are in this domain. The appropriate strategy for obvious problems, then, is simply to categorize the problem (“it’s one of those”) and apply the appropriate best practice solution.
Moving up the ordered side, we have complicated problems. These are problems where cause and effect is knowable in advance but where expertise and analysis are required first. This is the domain traditional project management is optimized for. Because the interactions between parts are predictable, complicated problems can be decomposed and reassembled. Detailed project plans can be created and executed. Many engineering problems are in this space. They’re governed by physical laws rather than human preferences and behavior, so they can be analyzed and calculated accurately in advance.
At the top of the unordered side are complex problems. Complex problems have an unknown relationship between cause and effect at the outset. Complex problems change as you solve them, often because you learn about the problem as you solve it. Typical examples include:
- new problems you’ve never solved before—you don’t know what you don’t know
- problems that involve integration with other systems outside your control—there’s nothing like actually integrating to reveal how other systems really work
- anything that depends on big things outside your control like markets, politics, or weather
- anything that depends on the future preferences and behaviors of humans—we’re terrible at predicting our future behavior in the abstract (“oh, now that I see it, I actually don’t want that, I want this…”)
It turns out that most of product development (e.g. software development) looks like this. This is why traditional project management has fared so poorly in this space.
The solutions for complex problems can’t be planned in detail in advance because the problems are unknown and emergent. Instead, complex problems require experimentation. The word for this strategy in Cynefin is probe. A probe is a small, safe-to-fail experiment—a prototype, a small release, or an MVP.
Unfortunately, the emergent nature of complex problems means that they make sense in retrospect, which tricks us into thinking they were actually complicated (Cynefin calls this retrospective coherence). Consider this common scenario: You’re facing a complex problem but don’t realize it, so you create a detailed plan for it as if it were complicated. Somewhere along the way, the problem changes, you learn something new, and the plan breaks. Because of a cognitive bias called the curse of knowledge, once you know something, it’s very hard to imagine not knowing it—it just seems obvious now. So, it’s natural to believe that thing that emerged could have been known at the outset and to say something like, “Next time we should plan better.” But, of course, you couldn’t have planned better—it was actually trying to solve the problem that caused that new learning to emerge.
People try to work around this by building in buffers and contingencies, but that’s still a fundamentally complicated approach to complex problems. It assumes analysis and planning are the right approach, just that they’ll be less than perfect. An approach native to complexity requires experimentation. It requires deliberately and actively going after uncertainty to get the system to reveal its order.
This is where Agile methods come in handy. Working iteratively in small slices, allows for small, safe experiments followed by adaptation based on learning.
Most large projects contain a mix of obvious, complicated, and complex work. When faced with that mix, most organizations tackle the obvious work first, proceed into the complicated work, and eventually take on the complex. This offers quick wins, progress right away. Unfortunately, it defers learning, creates an illusion of progress (as the progress on obvious work is unrepresentative of what will happen on the complex), leaves risk unaddressed, and ultimately saves the high-value work (because new = complex) for last, when schedules are inevitably compressed. Instead, we should immediately go after the core complexity of a project and work our way into the ordered side. This tackles risk and value right away and moves more and more towards real predictability. (I created Feature Mining, which is covered in our product ownership courses, as a technique for identifying a small slice of the core complexity to address first.)
As complexity in the world increases and as a larger share of work becomes complex, we should expect business to rely heavily on iterative, experimental approaches to work. But detailed planning persists because retrospective coherence fools us into thinking it ought to work better than it actually does.
Finally, the fourth kind of problem in the Cynefin framework: chaotic. Some problems are emergencies. In these cases, the problem solving strategy heavily favors action. We shouldn’t spend time experimenting and planning when a house is on fire—we should put out the fire! Later, the problem could move into the complex space, and we might experiment to try to understand the fire and, hopefully, identify ways to prevent future fires, but when the problem is in the chaotic space, the goal is to act, to solve the problem as quickly as possible. This need for immediate and correct action is why emergency responders spend so much of their time practicing and why they overstaff for high responsiveness.
Things go well when we know what kind of problem we’re facing and apply the appropriate strategy. But often we don’t know. And that’s what the middle space in the Cynefin diagram is about. The so called disordered space is where we are when we don’t know where we are.
Individuals have a preferred problem solving strategy. Some (like me) enjoy complex problems and the experimentation they require. Others like complicated problems and enjoy getting all the parts in order and creating detailed plans (they often become project managers). Some like having recipes and best practices and do well with obvious problems. Some thrive on chaos and gravitate towards fields like emergency medicine.
When you’re in the disordered space, you run the risk of applying your preferred strategy whether it first the problem or not. I might drive other people crazy trying to experiment on obvious, well-solved problems. Someone who likes complicated problems might over-plan for a complex problem. Someone who likes chaotic problems might just jump in and act on a non-chaotic problem, creating chaos!
So, the goal in the disordered space is to get out. Identify what kind of problem you’re facing before you try to solve it.
Identifying the problem is most difficult on the complex vs complicated distinction. Chaotic problems yell at you. Obvious problems are familiar. But complex and complicated are easy to confuse. In that case, favor the complex approach. Probing a complicated problem is safer than trying to analyze and plan for a complex problem. So, when I think I’m facing a complicated problem but I’m not entirely sure, I ask myself, “What part of this could surprise me?” and I go there first. If it was in fact complicated, I’ve just made progress on the solution. But if it was actually complex, I’ve discovered that faster than I otherwise would have.
Key takeaways:
- In business, more problems are complex than our common approaches would suggest. We’d do well to probe more and plan less.
- If you don’t know what kind of problem you’re facing, figure that out before you go too far.
- Know your preference and know what it looks like when you’re using it in the wrong domain so you can recover faster.
- Agile approaches like Scrum work well in the complex and complicated domains. Traditional project management works well in the complicated domain. For obvious and chaotic work, ticketing systems and manufacturing approaches are the right tools.
Last updated